多分野の融合研究により、モビリティの「流れ」をデザインする。

辻本諭(つじもとさとし)
幾何学ネットワーク解析チーム・リーダー
京都大学 情報学研究科 准教授
1997年に早稲田大学大学院理工学研究科 博士後期課程を修了、博士(工学)。早稲田大学 助手、大阪大学 助手、京都大学 講師などを経て、2009年より現職。専門は応用数学。とりわけ、特殊関数および直交多項式の理論とその応用に関する研究に従事。
モビリティ社会では、大量のヒト・モノ・サービスがスムーズに流れることが重要となる。幾何学ネットワーク解析チームの辻本准教授は、こういったモビリティ社会の「流れ」を予測・デザインする研究に取り組んでいる。チームには幾何学や生命科学など、多分野の専門家が在籍。さまざまな視点から流れを見つめ、予定調和ではない新たな「化学反応」を起こそうとしている。どういった信念で研究に取り組んでいるのか、辻本准教授に話を聞いた。
※本記事は「モビリティ基盤数理研究ラボ」の前身となる「モビリティ基盤数理研究ユニット」時のものになります
異分野をむすぶ「可積分系」に魅せられて。
——はじめに、先生の専門分野について教えてください。
大きなテーマは「可積分系」と「直交多項式」です。名前を聞いたことはないかもしれませんが、どちらも身の回りで使われているんですよ。
——難しそうな名前ですね。具体的にはどういった研究分野なのでしょうか?
まず、「可積分系」について説明しましょう。これは「自然現象を表す複雑な方程式のうち、解く方法があるもの」です。
最初に、可積分系を理解する上で重要な「微分方程式」について説明させてください。海に現れる波の形、熱いお湯が冷める様子、雨粒が空から落ちてくる様子……。これら身の回りの自然現象は、「微分方程式」とよばれる数式(モデル)で表現できます。複雑な自然現象の本質を抽出して微分方程式で表現すれば、現象の理解に一歩近づくのです。さらに、この微分方程式を解けば、その現象の変化を予測できます。非常に便利ですよね。
実は微分方程式には、「線形」微分方程式と「非線形」微分方程式の2種類があります。「線形」微分方程式と「非線形」微分方程式では、数式の形が異なります。「線形」よりも「非線形」の方が複雑で難しい、とイメージしてください。実は、自然現象を表す微分方程式は、ほとんどが非線形です。そして、ほとんどの非線形微分方程式は解くことができません。
一方で、非線形微分方程式の中には工夫すれば解けるものもあります。これが、私の研究分野である「可積分系」です。解けるから、現象の変化を予測できる。そのため、可積分系は実社会のさまざまな分野で使われているんですよ。
——具体的にはどのような用途に使われるのですか?
身近なところでは、インターネット検索結果の表示順序を決めるアルゴリズムや、物理現象(波や超伝導など)の表現などです。また、可積分系はさまざまな顔をもっており、多くの異なる分野と関係しています。全く異なる分野を研究する過程で、意図せず同じ可積分系の方程式に行き着く場合もあるのです。物理の分野で提唱された波のモデルが実は可積分系だった、といったこともありました。これは、物理と数学が思わぬ形で融合した例ですね。別分野で発展してきた概念が思わぬ形で融合し、各分野に新しい考え方やものの見方が導入される。非常に面白いです。私自身、常に新鮮な気持ちで研究に取り組んでいます。
——先生はこれまで、可積分系の分野でどのような研究をされてきたのですか?
卒業論文以降、可積分系の微分方程式を「離散化」する方法を研究してきました。
微分方程式は「連続的」に変化する現象を記述する方程式です。通常、微分方程式を解くにはコンピュータを使用しますが、コンピュータは「離散的」な量(「0」と「1」)しか扱うことができません。そのため、微分方程式をコンピュータ上で解くには、方程式を変形して「とびとびの値にする(離散化する)」必要があるのです。「解ける」という性質を残したままうまく離散化できれば、さまざまなアルゴリズムで使えるようになります。
このほか、新しい可積分系の微分方程式を作る研究も進めています。コンパクトで計算量が少ない、多分野で役立つ方程式を作りたいですね。
——続いて、もうひとつの研究分野である「直交多項式」について教えてください。
直交多項式は、「直交性」とよばれる性質を満たす多項式です。直交性があれば、複雑な物事をパーツに分けて解析できます。例えば、話し声から特定の周波数の音だけを抜き出すことも可能です。
実は、直交多項式は可積分系とも密接な関係があります。直交多項式を調べた結果、新しい可積分系の微分方程式が見つかるケースもあるんですよ。
「流れ」を「箱」と「玉」で表現する。
——モビリティ基盤数理研究ユニットでの研究内容について教えてください。
「流れ」の本質をモデル化する方法や、作成したモデルを解析する方法を研究しています。モビリティ社会では、ヒト・モノ・サービスがスムーズに流れることが重要です。流れが悪くなって、宅配便の荷物が遅れたり電車がスムーズに出発しなかったりすると、モビリティ社会はうまく機能しなくなるでしょう。私たちの研究は、こういった流れを予測・整理・デザインする際に役立ちます。車の流れを解析して、渋滞や事故の場所を特定することもできるはずです。
——研究を進められる中で、工夫されている点はありますか?
ひとつは、モデルの作り方ですね。物やサービスにはさまざまな種類があるため、研究ではそれら全ての流れを表現できるモデルが必要です。そこで私たちは、あらゆるモノやサービスを「粒子」として抽象化し、「多体粒子系(多くの粒子が相互作用するモデル)」として表現することにしました。この多体粒子系を、先ほど説明した可積分系の微分方程式でモデル化するのです。
——ここで可積分系が登場するのですね。
はい。ただ、実は多体粒子系をモデル化した微分方程式は非常に複雑であり、解析が困難です。そこで、元の微分方程式の特徴を維持したままで、より簡単な別のモデルに変換する必要があります。ここからが特に面白いところです。なんと可積分系の微分方程式は、「箱」と「玉」のみからなる非常に単純な系(箱玉系)に変換できるのです。これは、玉を動かして流れを表現するモデルです。
——微分方程式を箱と玉にまで簡単にできるとは、驚きです!
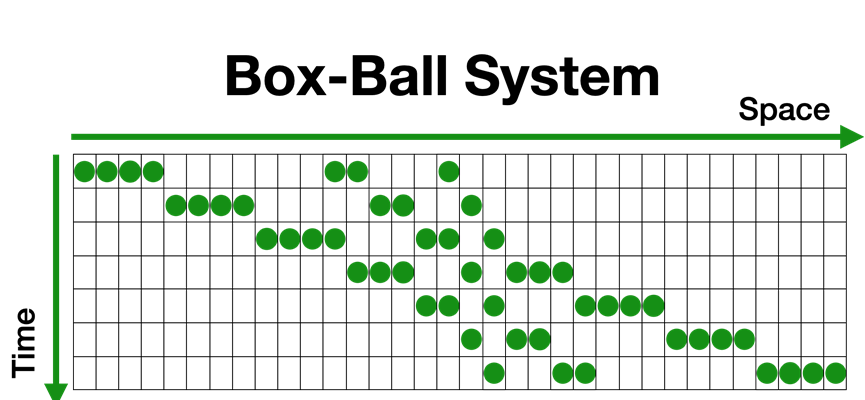
このように簡単化できる点が、可積分系の優れた特徴なのです。現在私のチームでは、「流れ」を表す箱玉系モデルの作成や、作成したモデルの解析手法の開発を行っています。これまでの研究で、作成した箱玉系モデルを一般化してかなり広い範囲に適用できることも分かりました。ただし、現在のモデルはまだ複雑性が高く、コンピュータ上で解析するのは難しい状態です。今後は、モデルの簡単化をさらに進めて、流れに関するさまざまな特徴量(人の位置など)を解析できるようにするのが目標ですね。
分野横断的な研究により、新たなものの見方を示したい。
——先生のチームには、多分野の専門家が参加されていると聞きました。どのように研究を進めておられるのでしょうか?
今回、幾何学、生命科学、ビッグデータ解析、シミュレーションなどの専門家を招待してチームを組みました。現在は、各々の専門分野を融合させて研究を進めています。例えば、広い意味での箱玉系の理論を用いて流れをモデル化や解析する際に、幾何学の視点を取り入れています。幾何学は、複雑なもの同士の関係性をざっくりと捉えるのに適した分野です。例えば、ドーナツとマグカップはどちらも穴がひとつ存在するので同じ形だと考える、といった具合ですね。幾何学の観点から流れを見れば、流れの移り変わりや関係性をラフに分類でき、新たな視点が得られるのではと考えています。また、生物の細胞ネットワークも、交通流や人流と同じように粒子として扱える可能性があります。そこで、細胞が動く様子を撮影した動画データをいただいて、研究に活用したりもしています。モビリティとは一見関係なさそうなことも積極的に取り入れている点が、私のチームの特徴かもしれませんね。
——今回のプロジェクトでは、長期的にどのような成果を目指したいと考えておられますか?
現在の研究を進めれば、人流を解析して人混みが少ないルートを提案する、といったことが可能になるでしょう。しかし、そういった研究は本ユニット以外でも多くの人が取り組んでいます。私たちが本当に目指しているのは、多分野を融合させた研究を行い、過去の価値観や考え方を超えた、新たなものの見方を生み出すことです。そういう意味で、実は予定調和ではない結果を一番期待しているんですよ。あえてモビリティという枠にはめずに研究を進めることで、モビリティだけを目標とした研究では到達できない領域に行けるはず。そうすれば、結果的にモビリティにも貢献できる。こういった信念で、日々研究に取り組んでいます。


